嘿,大家好!最近视频博主陶哲轩又带来了新内容,这次是个超实用的AI教程——
他手把手教大家如何仅通过GitHub Copilot来证明函数极限问题。
(更新频率真的是让人佩服o( ̄▽ ̄)d)
陶哲轩提到,他之前主要是把GitHub Copilot用来完成一些“花哨”的代码,但如果想用它来证明数学定理的话,还是需要人类来“正确引导”。
所以这次教学的重点就是:
教大家如何正确地引导GitHub Copilot。
他从函数极限的定义开始,逐步演示了求和、求差和求积定理的证明过程,分享了遇到的问题和解决方案,整个过程真的是细致入微。
接下来,我们具体看看吧。
一招鲜:Copilot代码补全加人工调整
首先,结论是,陶哲轩一直以来的观点是,GitHub Copilot等AI在数学定理证明中,更多是起辅助作用。
Copilot可以迅速生成代码框架和常见模式,这对新手特别有帮助,还能提示使用已有的库函数。
不过,在面临复杂的数学细节、特殊情况以及需要创造性解决方案的问题时,Copilot的准确性就会降低,这时就需要大量的人工干预和调整。
他认为,碰到复杂问题时,还是要结合纸笔推导,确保思路正确后再通过形式化的方式验证。
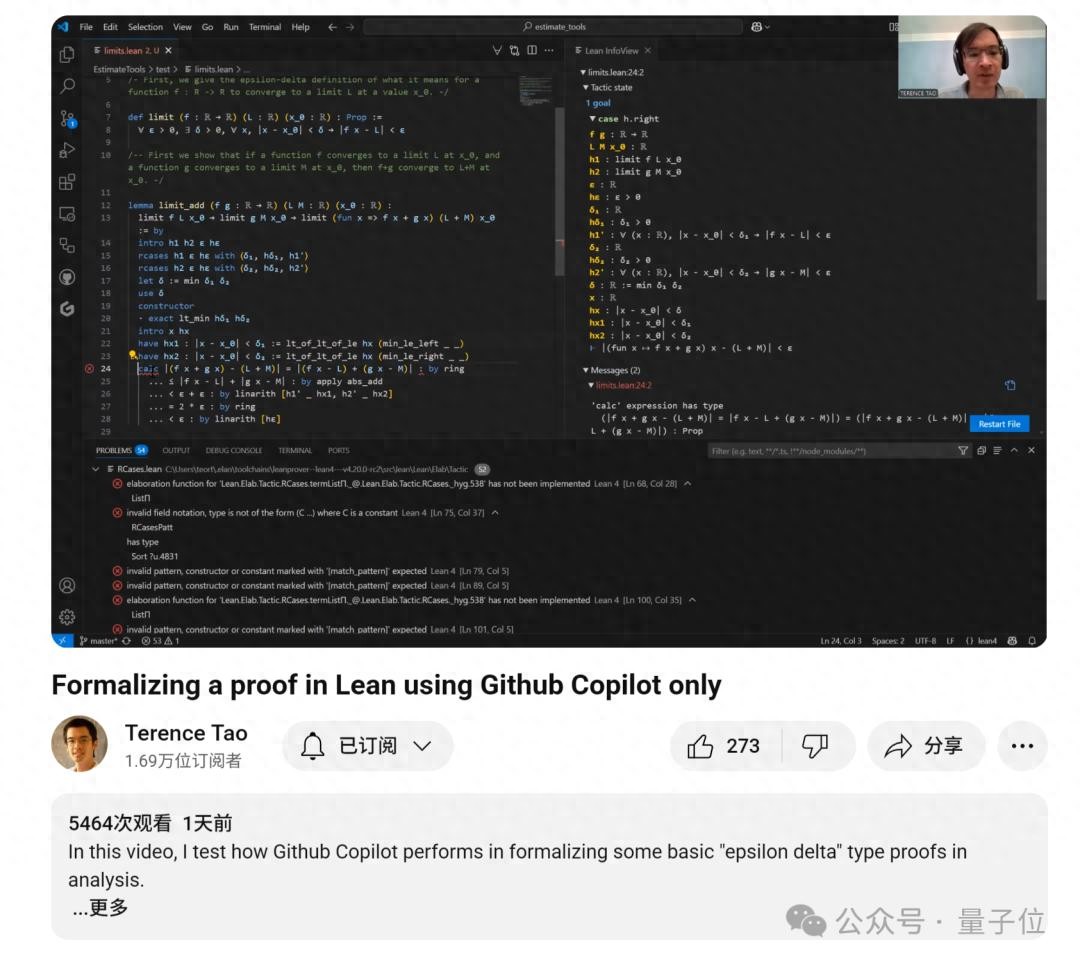
接下来是详细的证明过程。
首先,他定义了函数极限问题,即“设f是从实数到实数的函数,当x接近于x_𝜃时f(x)收敛于L”。
Copilot为这个极限的ε-δ定义提供了自动补全,但因为陶哲轩更喜欢用绝对值符号,所以他稍微调整了一下。
求和定理证明
接下来,他提出了第一个要证明的问题——函数极限的求和定理证明。
如果函数f在x_𝜃处收敛于L,函数g在x_𝜃处收敛于M,那么f+g在x_𝜃处收敛于L+M。
Copilot给出了正确的命题说法。
在证明的过程中,陶哲轩大量使用了“Copilot代码补全+人工手动调整”的方式。
比如,证明的第一步需要提取f和g收敛的ε-δ条件,特别是δ的选择要特别注意,得取δ₁和δ₂的最小值,以确保两个函数都能收敛。
可是,Copilot最初给出的证明方法在处理δ的正性验证时就显得不够严谨。
而且在证明不等式的部分,陶使用了计算块(calc block)来构建不等式的链条。虽然Copilot生成了基础结构,但在绝对值符号的处理和最后步骤上出现了差错。
这就需要他手动修正几个关键点:
去掉多余的绝对值符号
修正三角不等式的使用
调整最终的表达式
另外,面对数学分析中常见的ε损失问题,陶也尝试让Copilot用标准的方法(从一开始就用ε/2进行论证),但是发现生成的代码中ε依然是之前的两倍,因此又需要手动调整参数。
数学证明中的Copilot表现如何?
说白了,陶在使用Copilot时,经常在自动补全和自己手动调整之间来回切换。虽然Copilot能迅速生成代码结构,但一些重要的数学细节和严谨性,还是得靠他亲自把关。
值得注意的是,Copilot在后期的提示中建议使用Lean内置的add_sub_add_comm引理,这样可以简化重组过程。
这就说明,Copilot并不仅仅是个代码补全工具,它还能提醒开发者利用已经存在的库函数。
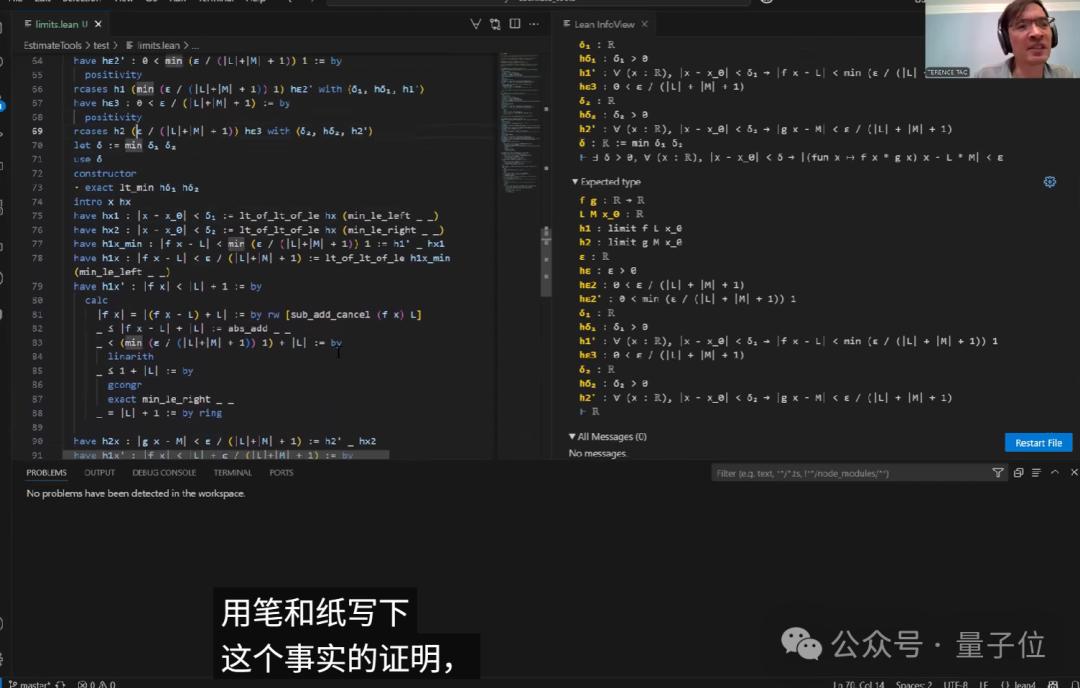
关于求差定理的证明
在他成功证明和的极限后,陶又想着用类似的方式来证明差的极限。
跟之前一样,Copilot能够生成大致正确的命题描述,并且沿用了之前的证明框架。
不过,在一个关键步骤上,它却犯了错误:使用了一个并不存在的sub_sub_anc方法。
虽然陶试图通过提示让它修复这个错误,但Copilot似乎记不住上下文,最终给出的解决方案也不太理想。
此外,在处理代数表达式时,陶原本希望能运用congruence策略来匹配等式的两边,但这个策略有点过于激进,简化得太多了。
在这个环节,Copilot的表现相对不太稳定,有时会虚构一些并不存在的方法。
最终,陶不得不亲自完成这个代数恒等式的证明。尽管这个恒等式在所有交换群中都成立,但Lean的数学库里却并没有直接的解决方案。
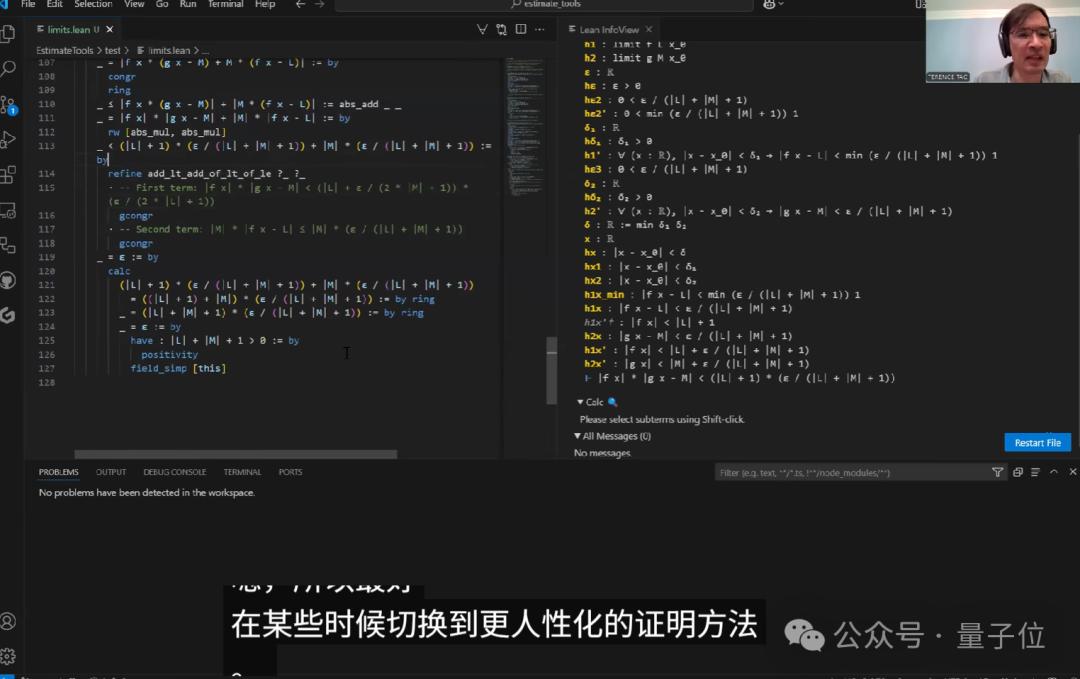
关于求积定理的证明
最后,陶对Copilot在函数乘积极限定理证明中的表现打了个B+。
总体来看,它完成了大部分工作,但在处理ε的分配和绝对值不等式时却出现了一些混乱。
首先,Copilot提出的策略是:
把f的近似误差设为ε/(2|M|+1),
把g的近似误差设为ε/(2|L|+1)。
陶哲轩认为这个思路是基本正确的,但在具体实现上出现了几个问题:
首先,在验证正性条件时,Copilot试图使用多个特定引理,实际上可以运用更通用的正性验证方法。(陶在这个部分做了手动调整)
数学探索中的小插曲
说到处理绝对值不等式,Copilot这家伙就犯了个小错误。它用了一种需要双方都严格不等的方法,结果在实际操作中却碰到了一道等式。陶哲轩试图帮助它纠正这个问题,然而给出的解决方案却并没有达到预期的效果。
与此同时,在最后证明的几个重要步骤中,尽管Copilot在整体上帮了大忙,但在处理那些复杂的数学细节时,还是需要人工来把关,以确保所有的结果都是准确的。
比如说,使用三角不等式来分解表达式,分别控制f(x)-L和g(x)-M的各个部分,以及处理交叉项L(g(x)-M)和M(f(x)-L)时,陶哲轩特别强调了在处理不等式和绝对值运算时,每个步骤的适用条件是至关重要的。
例如,在最后阶段遇到了一个小bug:Copilot假设M是正数,但这其实并没有什么依据。为了这个问题,陶也花了一些时间手动进行调整,他意识到,当问题的复杂性上升到一定程度时,Copilot的表现就不那么可靠了。
最后他得出了一个结论,面对这些情况,回归到传统的人工证明方法可能会更有效。
如果我能先用纸笔把完整的证明思路写下来,确保所有的ε参数都设置得当,然后再进行形式化验证,那效率绝对会更高。
总结一下,尽管Copilot这类工具在起初阶段确实能提供帮助,但关键在于知道什么时候用它,什么时候又该回到传统的方法。
再谈一件事
尽管这个教学过程得到了很多好评,但网友们的关注点似乎开始偏离了——
大家在线求助,更换录音设备。

看来油管的新晋博主确实还有提升的空间呢(doge)。
参考链接:
[1]https://www.youtube.com/watch?v=c1ixXMtmfS8
[2]https://github.com/teorth/estimate_tools/blob/master/EstimateTools/test/limits.lean
本文摘自微信公众号“量子位”,作者:关注前沿科技,36氪经授权发布。