嘿,视频博主陶哲轩又有新动态啦!这次他带来了一个“超简单”的AI教程——
一步步教你如何利用GitHub Copilot来证明函数的极限问题。
(这更新频率真是让人惊讶呢o( ̄▽ ̄)d)
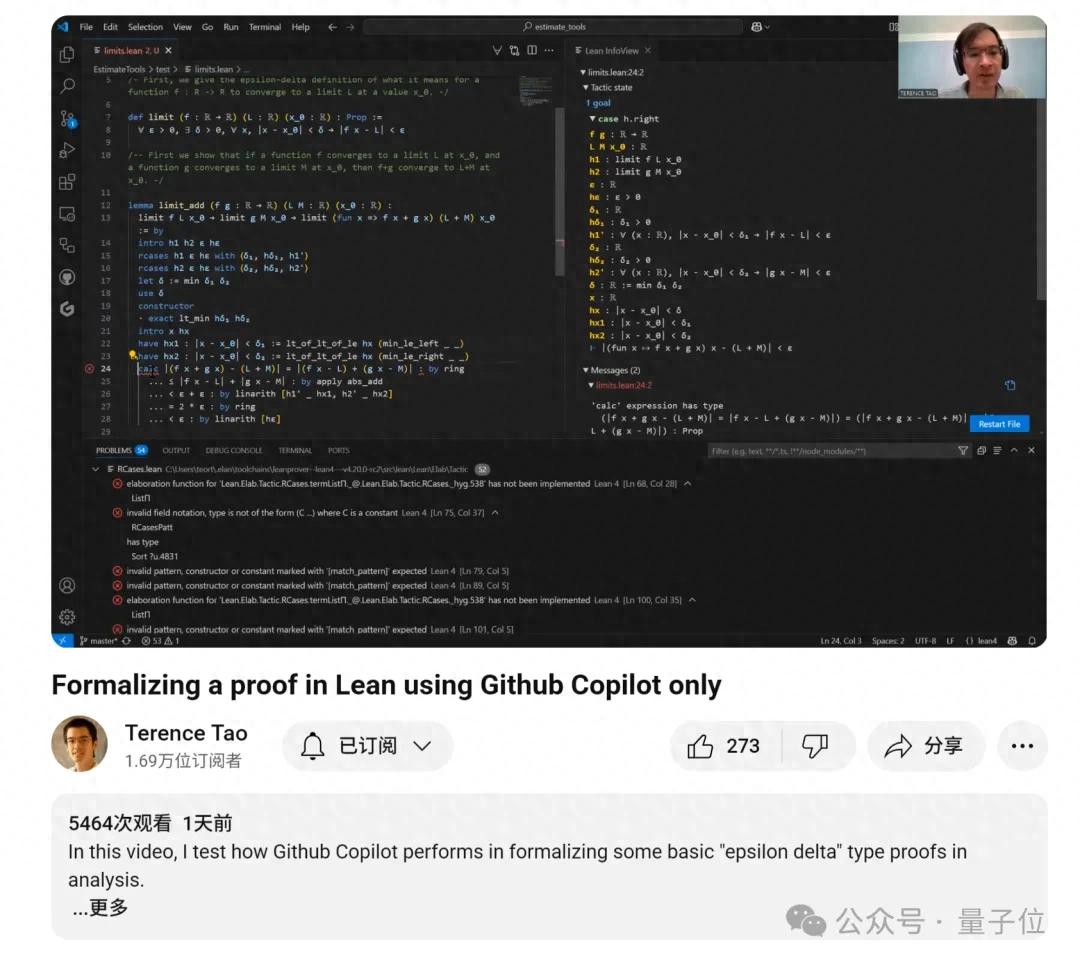
陶哲轩提到,以前他多是让GitHub Copilot处理一些“花里胡哨”的代码补全,然而要用它证明数学定理,确实得靠人类来指引方向。
所以,这次的教学重点就在于:
教大家如何有效引导GitHub Copilot。
他从函数极限的定义入手,逐步展示了求和、求差和求积的证明过程,还分享了自己在这个过程中遇到的难题和解决办法,整个过程非常细致。
接下来我们就具体看看吧。
秘诀:Copilot代码补全+人工微调
说实话,陶哲轩的观点没变,GitHub Copilot等AI在数学定理证明中,多数时候只是扮演一个“助手”的角色。
Copilot可以快速搭建代码框架,尤其对新手非常有帮助,还能提示使用一些现成的库函数。
不过,当碰到复杂的数学细节、特殊情况或需要创新性解决方案的问题时,Copilot的表现就不那么稳了,这时可得依靠大量的人力来调整。
在他看来,面对复杂的问题,结合纸笔好好推导,确保思路清晰后再进行形式验证是更为稳妥的做法。
探索函数极限的奥秘
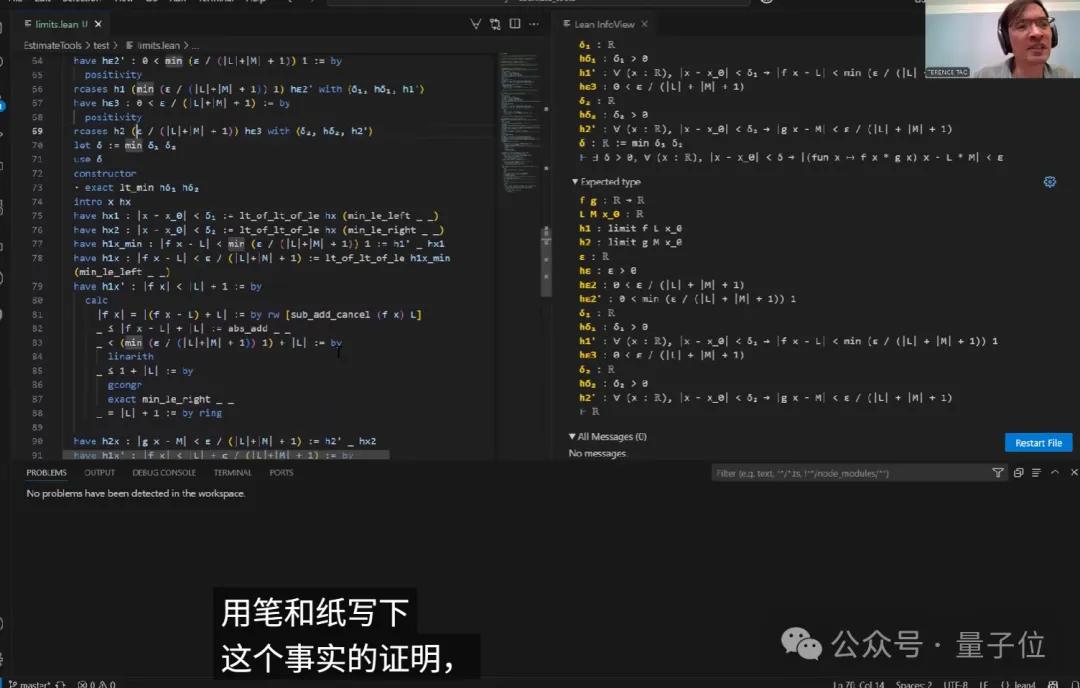
接下来,让我们看看他是怎么得出这些结论的。
最开始,他定义了一个关于函数极限的问题,简单来说就是“设f是一个从实数到实数的函数,当x接近x_时,f(x)会收敛到L”。
Copilot在这方面提供了极限的ε-δ定义,不过他更喜欢用绝对值来表达,所以稍微做了一些调整。
函数极限求和定理的证明
接着,他提出了第一个要证明的问题——函数极限的求和定理。
如果函数f在x_处收敛于L,函数g在x_处收敛于M,那么f+g在x_处收敛于L+M。
Copilot也给出了这一命题的准确表述。
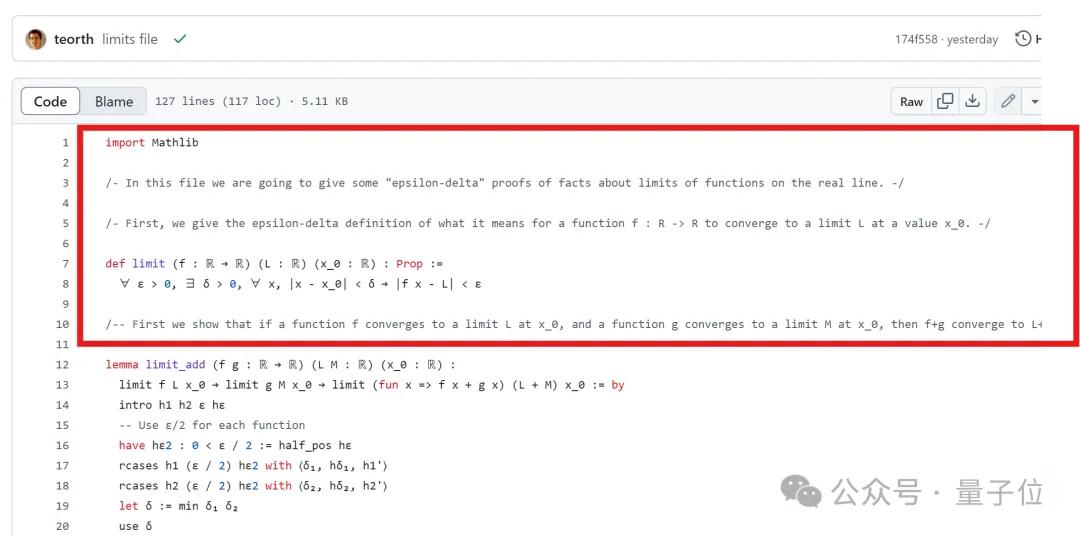
在证明的过程中,陶哲轩大量运用了“Copilot代码补全+人工调整”的方式。
探讨函数极限证明中的细节与Copilot的应用
在证明函数收敛的过程中,我们得先搞清楚f和g的ε-δ条件。这时候,选好δ的值就很关键了,通常我们会选择δ₁和δ₂中的最小值,以确保这两个函数能够同时收敛。
不过,Copilot最开始给出的证明方法有点问题,尤其是在验证δ的正性方面,显得不够严谨。(也就是判断某个数学结论是否为正)。在处理不等式的部分,陶哲轩用了一些计算块来构建不等式链。虽然Copilot能自动生成基本的框架,但在绝对值的处理和最后一步上还是存在一些偏差。
所以呢,有几个关键点需要手动修正:
- 去掉了多余的绝对值符号。
- 修正了三角不等式的应用。
- 调整了最终的表达式。
此外,为了应对数学分析中经常遇到的ε损失问题,陶也尝试让Copilot使用更标准的方法,像是从一开始就用ε/2来进行论证。结果发现,生成的代码中ε依然是原来的两倍,因此还得手动来调整这些参数。
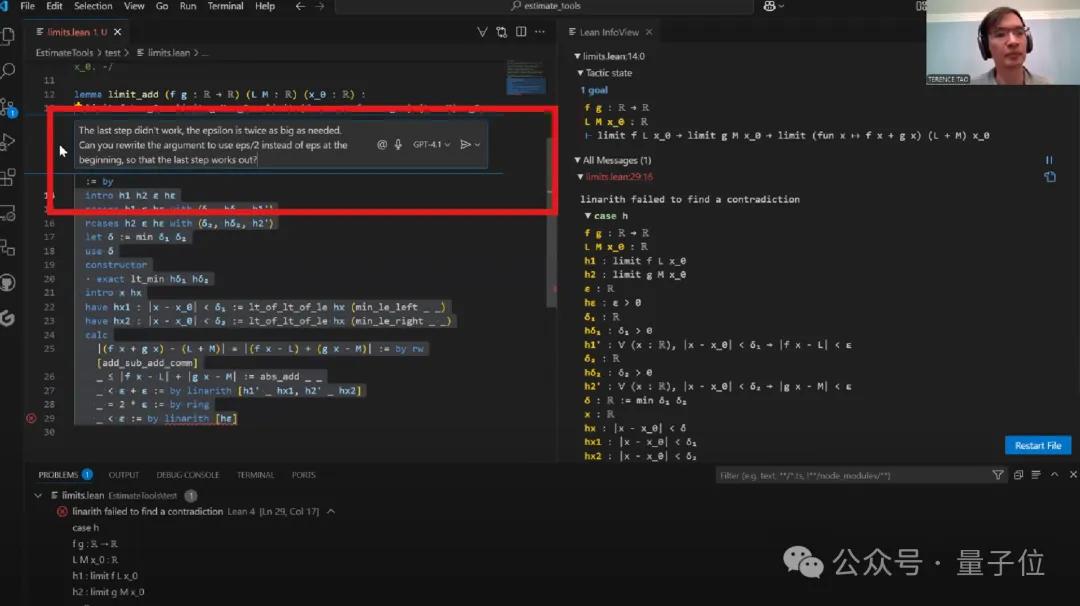
总体来看,陶哲轩在Copilot的自动补全和他的手动调整之间不断切换。虽然Copilot能迅速生成代码框架,但关键的数学细节和严谨性仍然需要人来把控。
值得一提的是,Copilot在后期还提示可以使用Lean自带的add_sub_add_comm引理,这样能让重组步骤变得更简单。
求差定理的证明过程
所以说,Copilot不仅仅是在帮你完成代码,它还可以提醒你利用手头已有的库函数,真的是个得力助手。
在证明和的极限后,陶决定尝试用相似的方法来证明差的极限。
就像之前一样,Copilot能生成一个基本正确的命题,并且还沿用了之前的证明框架,这一点很不错。
不过,在一个关键的步骤中还是出错了:它错误地引用了一个根本不存在的sub_sub_anc方法。
陶尝试通过提示来纠正这个错误,但可惜Copilot似乎记不住上下文,给出的解决方案也不太理想。
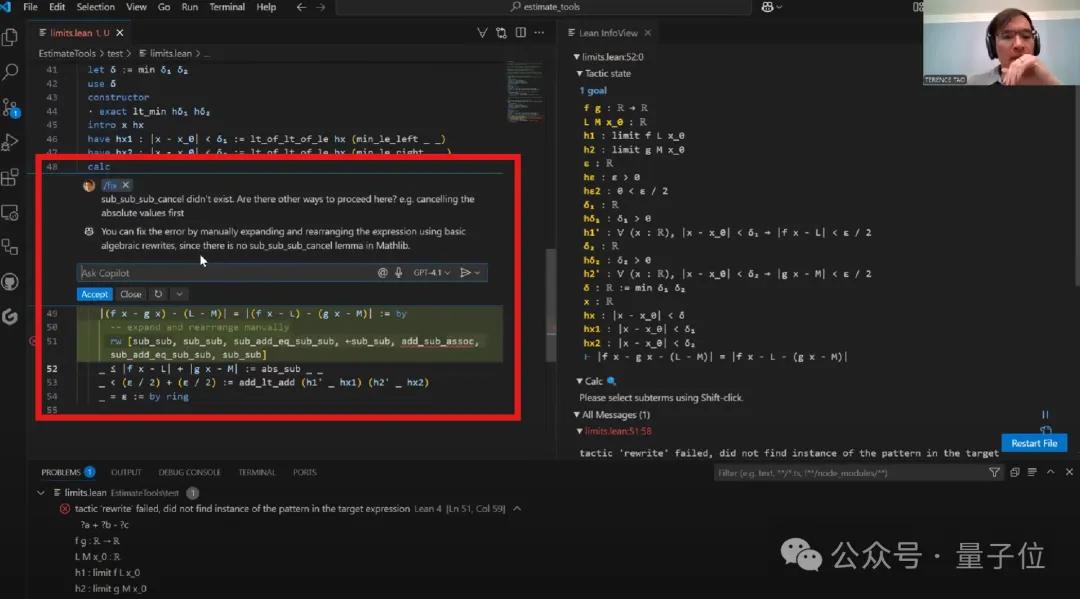
同时,在处理代数表达式时,陶原本希望采用congruence策略来匹配等式的两边,但这个策略有点过于激进,反而把问题简化得太过了。
在这一环节,Copilot的表现有些不稳定,有时候它会虚构一些根本不存在的方法。
最终,陶不得不手动完成这个代数恒等式的证明,虽然这个恒等式在所有交换群中都成立,但Lean的数学库里并没有现成的解决方案。
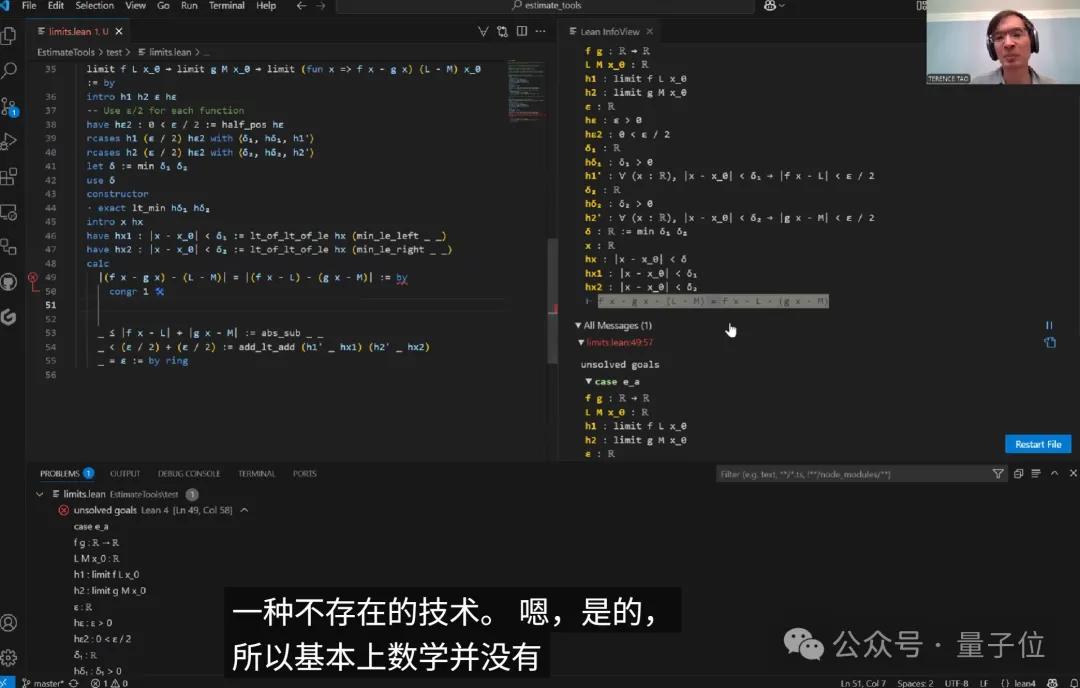
求积定理的证明过程
最后,陶对Copilot在函数乘积极限证明上的表现评分为B+。
总体来看,它完成了大部分的工作,不过在处理ε的分配和绝对值不等式时有点混乱。
首先,关于乘积极限的证明,Copilot提出了以下策略:
- 将f的近似误差设定为ε/(2|M|+1)
- 将g的近似误差设定为ε/(2|L|+1)
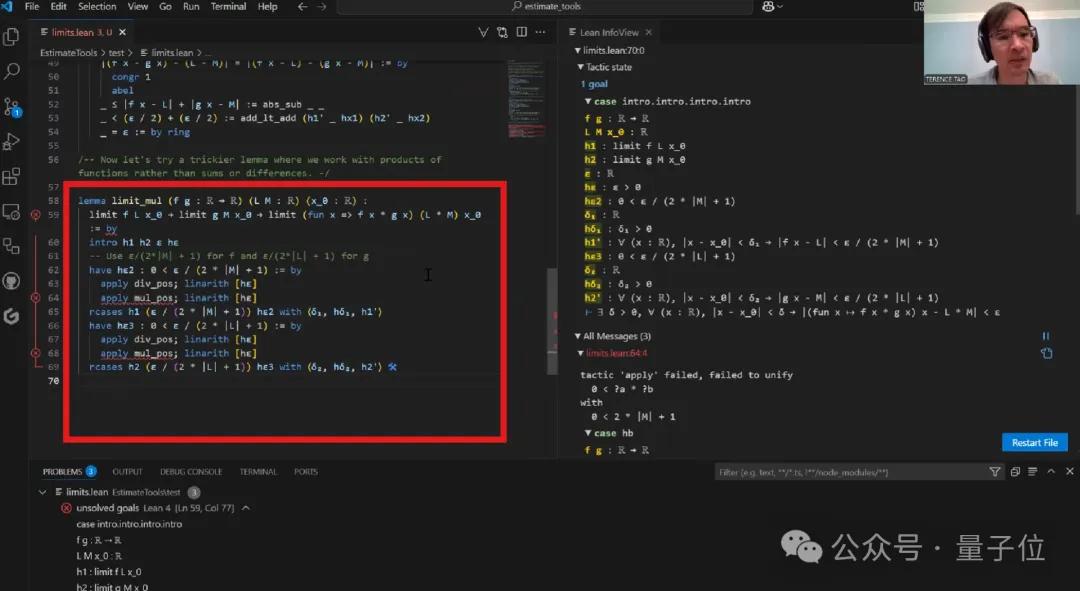
陶哲轩提到,这个思路大体上是对的,但在具体实施中碰到了一些问题:
首先,在验证正性条件时,Copilot用了很多特定的引理,其实可以用更通用的方式来验证正性。(陶对此做了手动调整)
其次,在处理绝对值不等式时,Copilot错误地采用了add_lt_add方法,而这个方法要求两边都必须是严格不等式,但实际情况中有一个等式存在。陶曾试图让Copilot纠正这个问题,但它给出的方案并不理想。
同时,在最后证明的几个关键步骤中,尽管Copilot在整体框架上提供了很大的帮助,但处理那些细腻的数学细节时,仍然需要人工介入,才能保证结果的准确性。
- 使用三角不等式来分解表达式
- 分别控制f(x)-L和g(x)-M的项
- 处理交叉项L(g(x)-M)和M(f(x)-L
数学问题中的小插曲与反思
陶哲轩提到,尤其是在处理不等式和绝对值的计算时,得特别留意每一步的适用条件。
比如在最后阶段碰到的一个小问题:Copilot生成的代码假设M是个正数,但实际上并没有这个条件。
对于这个问题,陶花了不少时间手动调整。他意识到,当问题变复杂时,Copilot的可靠性确实会下降。
最终,他得出的结论是,在这种情况下,回归传统的人工证明方法可能更有效。
如果我能先用纸笔把完整的证明思路写下来,确保所有的ε参数都设置正确,然后再进行形式化验证,效率会更高。
总结一下,像Copilot这样的工具在起步时确实帮助很大,但关键在于什么时候用它,什么时候又该回到传统的方法。
再说一件事
尽管这些教学得到了大家的好评,但网友们的关注点似乎逐渐偏离了主题——
大家在线上开始求换录音设备了。

看来新手博主们在油管上还真得多加练习呢(doge)。
— 完 —
量子位 QbitAI · 头条号签约
关注我们,第一时间获知前沿科技动态