最近,人工智能研究圈里掀起了一场关于大型推理模型能力极限的热烈讨论。在苹果公司发表论文质疑 DeepSeek-R1 这类大型推理模型的基本能力之后,不少研究者开始反驳,认为苹果的观点更像是在为自己在 AI 竞争中落后而找借口,简直是“吃不到葡萄说葡萄酸”。与此同时,关于研究方法的严谨性也遭到了不少质疑,甚至连 AI 模型都参与到了这场激烈的辩论里。
Open Philanthropy 的研究员 A. Lawsen 则是直接用 Claude Opus 发表了一篇犀利的反驳论文,标题为《思考幻觉的幻觉:对 Shojaee 等人 (2025) 的评论》(The Illusion of the Illusion of Thinking: A Comment on Shojaee et al. (2025))。

图丨相关论文(
之前的报道中我们提到过,苹果的研究团队通过让模型解答不同的谜题,发现 DeepSeek-R1、o3-mini 和 Claude-3.7-Sonnet-Thinking 等前沿大型推理模型在处理某些复杂问题时,准确率会大幅下滑。苹果团队认为,这说明这些模型并不具备真正的推理能力,而只是进行了一种模式匹配。比如模型在汉诺塔问题上可以做出多达 100 个正确的操作,但在逻辑推理游戏渡河问题上却只能给出不超过 5 步的正确解法。
不过,这篇反驳论文和其他质疑指出一个根本问题:苹果团队的发现其实主要反映了实验设计的局限,而不是模型本身的推理能力不足。第一个核心问题就是“物理令牌的限制导致了表象上的崩溃”。
Claude 的研究显示,在苹果所提到的失败点上,汉诺塔实验实际上超出了模型的输出 token 限制。论文中提到 X 用户 @scaling01 的复现实验,他发现模型的输出清楚表明:“模式继续,但为了避免过长,我将在这里停止”。
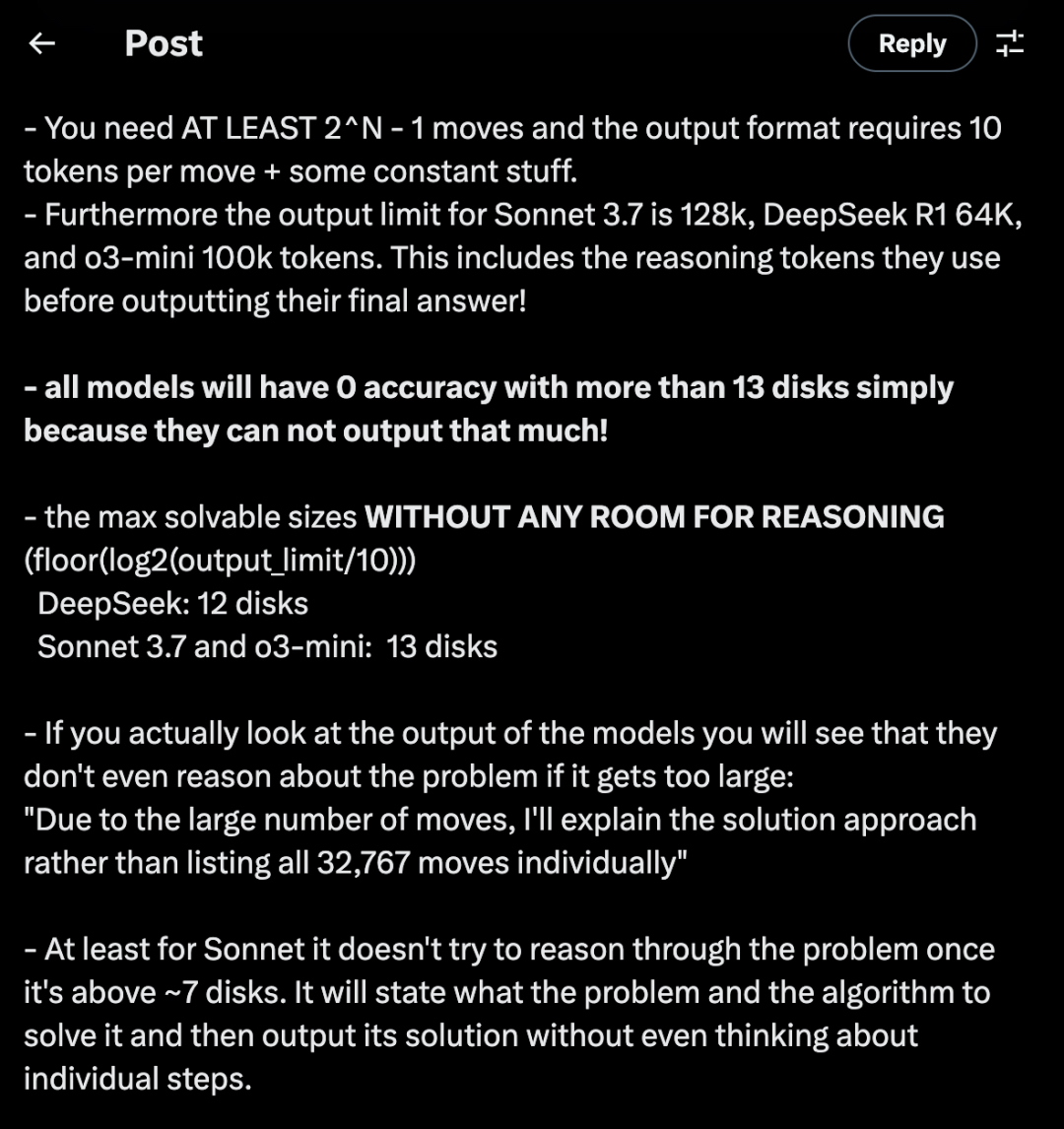
@scaling01 还指出,汉诺塔问题至少需要 2^N-1 次移动,而苹果使用的输出格式每次移动需要 10 个 token 和一些常量。更重要的是,不同模型在输出限制上差异很大:Sonnet 3.7 为 128k token,DeepSeek R1 为 64k token,o3-mini 为 100k token,这些限制包括模型在给出最终答案前所使用的推理 token。
图丨相关推文(
模型推理的复杂性:人类和机器的思考方式
其实,这些模型在处理超过13个盘子的情况下,准确率就会降到零。这完全是因为它们无法输出这么多的信息。@scaling01 计算得出,模型在没有推理空间的情况下,能处理的最大问题是:DeepSeek能解决12个盘子,而Sonnet 3.7和o3-mini只能处理13个盘子。当你观察模型的实际输出时,会发现如果问题的规模过大,模型甚至不会尝试进行推理,而是直接告诉你:“由于移动次数太多,我会给你一个解决方法,而不是逐一列出所有32,767次的移动。”
Claude的研究量化了这种情况,苹果的评估格式要求在每一步都输出完整的移动序列,结果导致了二次token的增加。如果每个序列的移动大约需要5个token,那么总的token需求公式可以简化为:T(N) ≈ 5(2^N – 1)^2 + C。在给定的token预算下,最大可解决的问题规模是可以通过这个公式预测的,而报告的“崩溃”现象正好符合这些物理限制。
有意思的是,@scaling01 还发现,对Sonnet来说,一旦问题超过7个盘子,它就不再尝试推理了。它会描述问题及其算法,然后直接给出解决方案,而不考虑每个步骤。这种行为模式进一步印证了Claude论文中的观点——模型确实理解问题和算法,但受限于输出格式。
更严重的情况出现在河流渡河实验中。Claude的论文指出,苹果团队测试了N≥6个行为者在船只容量为3的情况下,但这个问题早就有了数学上的解决方案:对于N>5且b=3的情况,根本没有解。通过自动将这些不可能的情况标记为失败,研究团队无意中展示了纯程序化评估的风险——模型得零分并不是因为推理失败,而是因为它正确地识别了问题是不可解决的。
从另一个角度来看,@scaling01分析了复杂性度量的问题。他指出,苹果研究使用最优路径长度作为问题复杂性的指标是个根本错误,因为这仅仅反映了解决方案的长度,而不告诉我们找到解决方案有多困难。即使汉诺塔的搜索空间很大,实际上你不需要进行任何复杂的搜索或回溯,因为只有一个简单的规则可用(大型语言模型知道),所以只有一条可行路径。
为了验证这个观点,@scaling01让o3和Gemini 2.5 Pro寻找其他更合适的游戏复杂性指标,结果一致地将游戏难度排为:河流渡河>>积木世界>跳棋跳跃>汉诺塔。这一排名与苹果研究的图表完全一致,这表明苹果团队的结论是“模型在较低组合深度的谜题上可能表现不佳,但在较高组合深度的不同谜题上却能成功”。这个发现其实并不让人意外,反而是完全在预料之中。
除了上述问题,还有研究者质疑使用汉诺塔这类知名谜题来测试推理能力的合理性。他们指出,如果担心数学和编程基准存在污染问题,为什么还要选择那些解决方案已经在训练数据中存在的著名谜题呢?汉诺塔的算法在模型的训练数据中频繁出现,这对模型帮助不大——毕竟它已经知道这个算法了。此外,推理模型是专门接受数学和编程方面的训练,而不是解谜训练。一些用户甚至说,这就像说“语言模型在写彼特拉克十四行诗方面没有比GPT-3.5好多少,所以我认为没有取得真正的进步”。
对于苹果研究所说的“复杂度阈值”意味着模型无法推理的观点,许多人提出了一个很有意思的问题:“有多少人类能坐下来正确计算出一千步的汉诺塔?”答案是非常少。这是否意味着那些做不到或不愿意做的人就没有推理能力呢?当然不是,他们只是在执行上千次枯燥的迭代中缺乏耐心和细致。正如一位Reddit用户所说:“人类能推理,并不代表他们能写下几千步的汉诺塔,反之亦然,写不下几千步并不代表他们没有推理能力。”
其实,把模型的行为看成人类的习惯,确实有点争议哦。还有一些评论者认为,像“不愿意”或者“寻找捷径”这样的说法其实是对模型行为的过度解读。他们认为,真正值得注意的是,当模型面对更复杂的8、9、10盘问题时,连基本的递归算法都难以使用,这就说明它的推理能力实际上是相当脆弱的,最多也就是在简单情况下模拟一下推理模式。
为了更清楚地说明,问题在评估方法而不是模型本身的能力,Claude的研究做了一个有趣的实验。他们对同一个模型进行了汉诺塔N=15的测试,不过换了一种表示方式:让模型输出一个可以打印解决方案的Lua函数,而不是详细列出每一步的移动。结果显示,在这个测试中,模型的准确率很高,甚至在不到5000个token的情况下就完成了。生成的解决方案成功地实现了递归算法,说明只要不要求详尽列举,模型的推理能力就能得到充分展现。
这篇论文总结的观点其实给我们带来了不少有价值的启示:模型无法生成超出上下文限制的token,程序化的评估可能会忽视模型的能力和谜题本身是否可解,此外,解决方案的长度也并不总是能准确反映问题的难度。不过,这些都无法支持他们关于“模型存在根本性推理局限”的主要观点。
“问题的核心或许并不在于大型推理模型的推理能力,而是在于我们的评估体系是否能将推理能力与单纯的‘打字’能力区分开。”
参考资料:
1.https://arxiv.org/pdf/2506.09250v1
2.https://www.seangoedecke.com/illusion-of-thinking/
3.https://x.com/scaling01/status/1931783050511126954
运营/排版:何晨龙









苹果的研究似乎忽视了模型输出限制的问题,简单的实验设计可能导致了误解。反驳论文指出了深层次的逻辑,其实模型并非完全失效。期待更深入的探讨!
苹果的实验设计确实存在局限性,忽略了推理过程中的输出限制,导致了不准确的结论。Claude的反驳很有说服力。
苹果的研究在实验设计上确实存在不足,未能全面考虑模型的输出限制。Claude的反驳深入浅出,让人重新思考推理模型的真实能力。
苹果的实验设计确实存在偏差,未考虑到模型的输出限制,导致结论不够准确。Claude的反驳很有深度,值得深入研究。
在大模型的推理能力问题上,苹果的实验设计显然有待商榷,Claude的反驳让人对模型的真实能力有了新的认识。期待更多深入的讨论与研究。
苹果的研究在推理模型上存在明显的设计缺陷,Claude的反驳为我们提供了更全面的视角。确实需要对实验条件进行更深入的思考。